Geometry Cheat Sheet: Triangles
In each Cheat Sheet, I’ll cover, as succinctly as possible, every rule you absolutely must know to solve problems in a single area found on standardized tests.
Learning these rules isn’t a substitute for developing higher-order problem-solving and strategic thinking skills; rather, it’s a necessary precondition and foundation for all of that strategizing to take place. This Cheat Sheet lists the minimum requirements to get your foot in the door. It’s the price of admission.
If you’re taking any test involving geometry, here’s what you need to know about triangles:
Table of Contents
- Lines and Angles
- Triangles
- Quadrilaterals
- Other Polygons
- Circles
- 3-D Geometry
- Coordinate Geometry
Triangle Basics
Area ![]()
Total angle measure ![]()
The Pythagorean Theorem:
- For a right triangle with side lengths
 ,
, 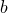 , and
, and  ,
, 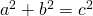 , where
, where  is the hypotenuse (the longest side).
is the hypotenuse (the longest side).
The Triangle Inequality:
- For any with side lengths
 ,
, 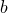 , and
, and  ,
, 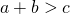 ,
, 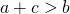 , and
, and 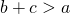 .
.- (The sum of the lengths of any two sides must exceed the length of the third side.)
This is not a triangle.
Special Triangles
Common Pythagorean Triples
- Any multiple of a Pythagorean triple is also a Pythagorean triple.
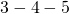 /
/ 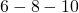 /
/ 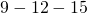 /
/ 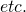
-
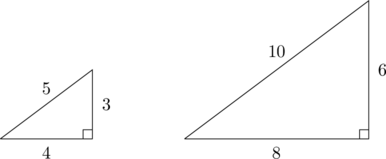
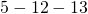 /
/ 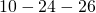 /
/ 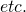
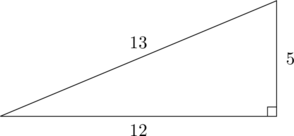
The ![]()
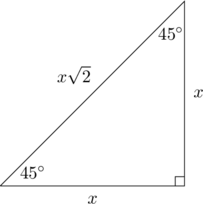
![]() Isosceles Right Triangle
Isosceles Right Triangle
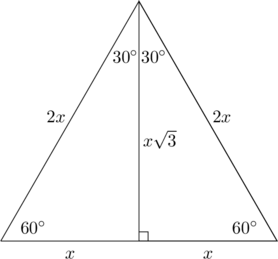
The Equilateral Triangle and the ![]()
![]() Right Triangle
Right Triangle
- An equilateral triangle has three sides of equal length and three angles of equal
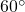 measure.
measure.
- Area of an equilateral triangle (with side length
 )
) 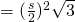 .
.
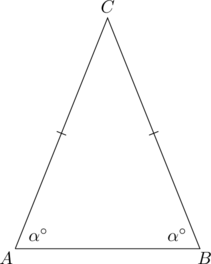
Isosceles Triangles
- An isosceles triangle has at least two sides of equal length.
- The angles opposite the equal sides of an isosceles triangle are equal.
Triangle Similarity
Similarity Basics
- Two objects are similar if they have the same shape, aside from scaling. In other words, similarity means that either object can be scaled up or down (and possibly flipped) to be identical the other.
- If two triangles are similar, then all of their corresponding angles are equal and all of their corresponding lengths scale by a common scaling factor,
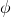 . Furthermore, the triangles’ areas scale by the factor
. Furthermore, the triangles’ areas scale by the factor 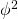 .
. - Note: Every geometric figure has similar versions, but triangles are the most-tested shapes on similarity questions.
Establishing Similarity in Triangles
- Similarity in triangles may be established using Angle-Angle-Angle, Side-Side-Side, or Side-Angle-Side comparison.
- Note: Similarity is most commonly tested on standardized tests using Angle-Angle-Angle similarity.
- Angle-Angle-Angle
-
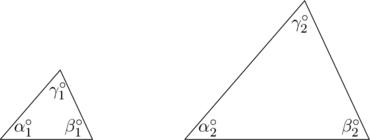
- The two triangles are similar if
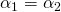 ,
, 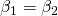 , and
, and 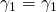 .
.
- Side-Side-Side
-
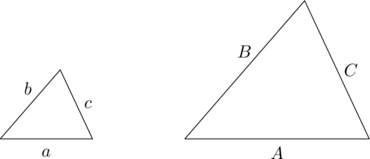
- The two triangles are similar if
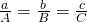 .
.
- Side-Angle-Side
-
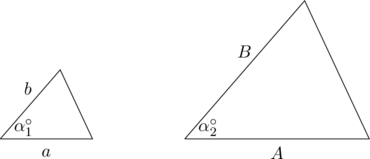
- The two triangles are similar if
 and
and  .
. - Note: Side-Angle-Side similarity requires that the equal angles must be located between the pair of corresponding sides.
Bonus: Common Cases of Similarity
- Parallel Lines
-
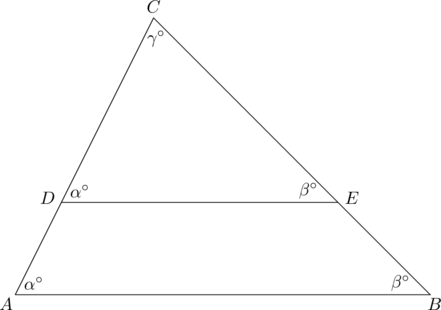
![]() is parallel to
is parallel to ![]() .
.
- Triangles
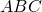 and
and 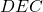 are similar, by angle-angle-angle similarity (shown above).
are similar, by angle-angle-angle similarity (shown above).
- Right Triangle with Height to Hypotenuse
-

- Triangles
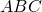 ,
, 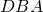 , and
, and 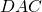 are similar, by angle-angle-angle similarity (shown above).
are similar, by angle-angle-angle similarity (shown above).
Tags: ACT, Cheat Sheet, Geometry, GMAT, GRE, Math, SAT, Triangles