LSAT Question Analysis #2
Building off the formal logic posts of the last two weeks, today we’re going to discuss the LSAT logic game found at PrepTest 58, Section 3, Questions 7-12 (10 New LSAT, page 241).
This is a fairly simple In-and-Out game (also known as a Selection game). Such games often involve heavy doses of arrow diagramming, and this one is no exception. Take a quick read of the setup and then let’s turn our attention to the rules.
…
…
…
…
…
The rules of this game can be diagrammed in straightforward fashion as follows:
- 1.
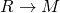
- 2.
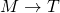
- 3.
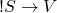
- 4.
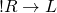
- 5.
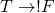
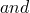
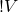
Let’s turn to the questions now.
Question 7
The first question of this game is known as a Complete and Accurate List question. These relatively easy “could be true” questions begin most LSAT logic games and serve to introduce the test-taker to the rules and the structure of the game setup. Given that function, a Complete and Accurate List question tends to make itself easy to identify by using the words “complete and accurate list” in its prompt and to employ nearly all of the rules given by its game setup so that the test-taker can check his or her basic understanding of those rules before moving forward. In fact, the Law School Admission Council itself has described questions of this type as “orientation” questions.
In light of their generally helpful nature, these questions ought to be basically “guaranteed points” for practiced LSAT-takers and should be doable in not much more than 30 seconds each. The proper method for achieving such positive results is to address each rule in turn, applying it to every answer choice and eliminating those choices that violate that rule. Students may even wish to note violated rule numbers next to eliminated wrong answer choices. This approach is far more efficient and less error-prone than the alternative of starting from the answer choices for this question type.
After identifying that Question 7 is, in fact, a Complete and Accurate List, go back to the rules and grab Rule 1. This rule states that ![]() . Now, apply that rule to each answer choice in turn. Rule 1 doesn’t apply to Answer A, since A doesn’t mention
. Now, apply that rule to each answer choice in turn. Rule 1 doesn’t apply to Answer A, since A doesn’t mention ![]() (recall that
(recall that ![]() says nothing when
says nothing when ![]() is absent). Answer B contains
is absent). Answer B contains ![]() , so it will be eliminated unless it also contains
, so it will be eliminated unless it also contains ![]() . However, B does contain
. However, B does contain ![]() , so it gets to stay. C doesn’t contain
, so it gets to stay. C doesn’t contain ![]() , so move along. D contains
, so move along. D contains ![]() but not
but not ![]() , so D is out. Finally, E doesn’t contain
, so D is out. Finally, E doesn’t contain ![]() , so it stays as well. This whole process, with practice, takes perhaps five seconds. After consideration of Rule 1, the answer choices for Question 7 should look like this:
, so it stays as well. This whole process, with practice, takes perhaps five seconds. After consideration of Rule 1, the answer choices for Question 7 should look like this:
A
B
C
D 1
E
Rule 2 states that ![]() . Answer A doesn’t contain
. Answer A doesn’t contain ![]() . Answer B contains
. Answer B contains ![]() , but it doesn’t contain
, but it doesn’t contain ![]() , so it’s out. Answer C doesn’t contain
, so it’s out. Answer C doesn’t contain ![]() . Answer D is already out (and doesn’t contain
. Answer D is already out (and doesn’t contain ![]() anyway). Answer E doesn’t contain
anyway). Answer E doesn’t contain ![]() . After two rules, the answer choices for this question should look like this:
. After two rules, the answer choices for this question should look like this:
A
B 2
C
D 1
E
Rule 3 says ![]() . Answers A, C, and E all contain
. Answers A, C, and E all contain ![]() , so this rule doesn’t eliminate anything that remains (it does eliminate B again, but that’s neither here nor there). With five rules, there had to be one that didn’t eliminate anything. This rule was the one.
, so this rule doesn’t eliminate anything that remains (it does eliminate B again, but that’s neither here nor there). With five rules, there had to be one that didn’t eliminate anything. This rule was the one.
Rule 4 says ![]() . Answer A doesn’t contain
. Answer A doesn’t contain ![]() , and it doesn’t contain
, and it doesn’t contain ![]() either, so cross it off. Answers C and E don’t contain
either, so cross it off. Answers C and E don’t contain ![]() , but they do both contain
, but they do both contain ![]() , so they’re not eliminated. After four rules, the answer choices should look like this:
, so they’re not eliminated. After four rules, the answer choices should look like this:
A 4
B 2
C
D 1
E
So it all comes down to Rule 5, which states that ![]()
![]()
![]() . Answer C contains
. Answer C contains ![]() , but it does not contain either
, but it does not contain either ![]() or
or ![]() , so it’s okay. Answer E also contains
, so it’s okay. Answer E also contains ![]() , but this answer includes
, but this answer includes ![]() as well. That’s a violation of Rule 5, so cross E off.
as well. That’s a violation of Rule 5, so cross E off.
A 4
B 2
C
D 1
E 5
Having checked all the rules and eliminated all but one answer choice, we’ve arrived at our answer. The correct answer is C.
Question 8
The prompt for Question 8 provides additional information: ![]() is in. In such cases, it’s best to turn to the rules again, instead of the answer choices, and to attempt to link the new information as much as possible. To do so, look for rules that use
is in. In such cases, it’s best to turn to the rules again, instead of the answer choices, and to attempt to link the new information as much as possible. To do so, look for rules that use ![]() as a condition. Remember the consider both the as-written and contrapositive forms as possibilities.
as a condition. Remember the consider both the as-written and contrapositive forms as possibilities.
- 1.
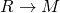
- 2.
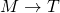
- 3.
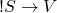
- 4.
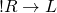
- 5.
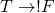
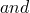
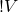
None of the rules as written appear to use ![]() as a condition, but the contrapositive of Rule 5 will work. It says, in part, that
as a condition, but the contrapositive of Rule 5 will work. It says, in part, that ![]() . (Rule 3 is useless here; it mentions
. (Rule 3 is useless here; it mentions ![]() only as a consequence, and its contrapositive instead uses
only as a consequence, and its contrapositive instead uses ![]() as its condition.)
as its condition.)
We can make an In-and-Out table to track our progress:
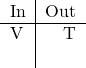
Since no other rules use ![]() in the desired manner, next look for rules that begin with
in the desired manner, next look for rules that begin with ![]() . Once again no rule appears to work as written, and once again the contrapositive swings to the rescue. Rule 2 is equivalent to
. Once again no rule appears to work as written, and once again the contrapositive swings to the rescue. Rule 2 is equivalent to ![]() . Our table becomes:
. Our table becomes:
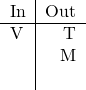
No other rules use ![]() , so
, so ![]() is up next. This time it’s the contrapositive of Rule 1 that we want. That contrapositive tells us that
is up next. This time it’s the contrapositive of Rule 1 that we want. That contrapositive tells us that ![]() .
.
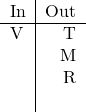
At last, we’ve gone far enough. We used rules 5, 2, and 1 and specifically excluded using Rule 3. We could go a step further with Rule 4 and discover that ![]() is in as well, but it’s not needed. Eliminate wrong answers as follows: Answer A uses
is in as well, but it’s not needed. Eliminate wrong answers as follows: Answer A uses ![]() , so it’s out. Answer C uses
, so it’s out. Answer C uses ![]() so it’s gone as well. Answers D and E both use
so it’s gone as well. Answers D and E both use ![]() , so they’re out too. Only Answer B remains, so Answer B must be correct.
, so they’re out too. Only Answer B remains, so Answer B must be correct.
Question 9
Here’s another question offering additional information: ![]() is out. We proceed as before, even using many of the same rules in many of the same ways (our first step beyond
is out. We proceed as before, even using many of the same rules in many of the same ways (our first step beyond ![]() last time brought us directly to
last time brought us directly to ![]() ).
).
![]() (Rule 2).
(Rule 2).
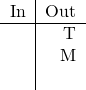
![]() (Rule 1).
(Rule 1).
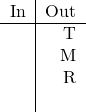
![]() (Rule 4).
(Rule 4).
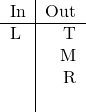
Whoops, we went one statement beyond what we needed again. For a “must be” question like this one (“cannot be true” = “must be false”), we’re just looking for the right answer, and we could have stopped as soon as we discovered that ![]() was out.
was out.
The right answer is C.
Question 10
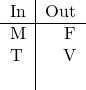
Got the hang of it yet? Well, here we go again. Question 10 adds the fact that ![]() is in.
is in.
![]() (Rule 2).
(Rule 2).
![]()
![]()
![]() (Rule 5).
(Rule 5).
![]() (Rule 3).
(Rule 3).
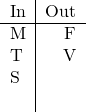
We can go no further, so we probably have the answer at this point. Let’s see… In a “could be true” we eliminate, and we can eliminate answers A, C, D, and E using the last chart above. Thus, Answer B is correct.
Question 11
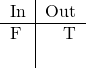
Wow, this game is repetitive. Question 11 says ![]() is in. I could practically copy/paste the rest:
is in. I could practically copy/paste the rest:
![]() (Rule 5).
(Rule 5).
![]() (Rule 2).
(Rule 2).
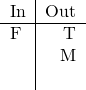
![]() (Rule 1).
(Rule 1).
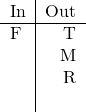
![]() (Rule 4).
(Rule 4).
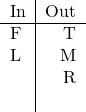
![]() is in. That’s A.
is in. That’s A.
Question 12
Finally we get a question that’s a little bit different (but hey, practice is always good, right?).
This is a specialized question type called a Counting Question that shows up on a lot of In-and-Out games, and I’ll be going into far more depth on these in a freestanding blog post at some point, so I’ll keep it relatively brief for the time being. Suffice it to say that whenever we’re asked, as here, to consider a minimum selection of items (“at least one”) we should look for rules of the type ![]() and entirely ignore rules of the type
and entirely ignore rules of the type ![]() .
.
Here, there are two rules that look like what we want:
- 3.
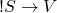
- 4.
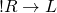
The contrapositives are:
- 3.
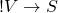
- 4.
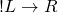
If we don’t have ![]() , then we have
, then we have ![]() , and if we don’t have
, and if we don’t have ![]() , then we have
, then we have ![]() . In other words, we need either
. In other words, we need either ![]() or
or ![]() . Sadly, no answer choice is quite that simple.
. Sadly, no answer choice is quite that simple.
Likewise, if we don’t have ![]() , then we have
, then we have ![]() , and if we don’t have
, and if we don’t have ![]() then we have
then we have ![]() . So we need either
. So we need either ![]() or
or ![]() . Unfortunately, that option doesn’t show up either. We’ll have to keep looking.
. Unfortunately, that option doesn’t show up either. We’ll have to keep looking.
To take the next step, link these two rules to any applicable rules NOT of the form ![]() . The available options are Rule 1 and Rule 2:
. The available options are Rule 1 and Rule 2:
- 1.
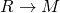
- 2.
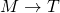
Rule 2 doesn’t link at all, but Rule 1 links to Rule 4:
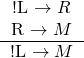
And, equivalently, ![]() . So we need either
. So we need either ![]() or
or ![]() ; check the answers again, and there it is! Answer B says exactly what we want, and it’s correct.
; check the answers again, and there it is! Answer B says exactly what we want, and it’s correct.
Tags: Analytical Reasoning, Complete and Accurate Lists, Counting (In-and-Out), Formal Logic, In-and-Out Games, LSAT, Question Analysis