Formal Logic 102: Contrapositives, the Transitive Property, and an LSAT Example
- * We learned that formal logic is an important part of the LSAT.
- * Arguments were broken down into propositions, which were shorthanded by capital letters and manipulated using operators.
- * Finally, negation and arrow diagrams burst onto the scene, leading to a shocking revelation:
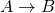 says nothing about what happens in the “not
says nothing about what happens in the “not 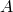 ” case!
” case!
But what other arrow diagram is equivalent to ![]() ? How can arrow diagrams be combined? Will we ever finally see an LSAT question example? Does Anthony have his umbrella?
? How can arrow diagrams be combined? Will we ever finally see an LSAT question example? Does Anthony have his umbrella?
These questions and more will be answered… tonight.
If It Isn’t About the Contrapositive, Then It Isn’t This Section
Is the statement ![]() equivalent to the statement
equivalent to the statement ![]() ? As one might suspect based on the Raining
? As one might suspect based on the Raining ![]() Umbrella example, it is not. In one case (Raining
Umbrella example, it is not. In one case (Raining ![]() Umbrella) I might be rocking the umbrella on a bright sunny day. In the other case (Umbrella
Umbrella) I might be rocking the umbrella on a bright sunny day. In the other case (Umbrella ![]() Raining) that’s impossible, but I might be getting wet. The statement
Raining) that’s impossible, but I might be getting wet. The statement ![]() isn’t the same either — we’ve already seen that
isn’t the same either — we’ve already seen that ![]() provides no information about the case in which
provides no information about the case in which ![]() is false.
is false.
One might wonder, then: Is there any other arrow diagram that actually is equivalent to the statement ![]() ? As you might imagine based on this line of inquiry, we’re in luck.
? As you might imagine based on this line of inquiry, we’re in luck.
The arrow diagram ![]() can be shown using truth tables to be wholly equivalent to the statement
can be shown using truth tables to be wholly equivalent to the statement ![]() . That is,
. That is, ![]()
![]()
![]() . This result is in fact so important that
. This result is in fact so important that ![]() is worthy of a name. It is known as the contrapositive.
is worthy of a name. It is known as the contrapositive.
To produce the contrapositive of a statement, reverse the order of the propositions, and then negate each term.
Returning to the umbrella example, recall that Raining ![]() Umbrella. Flipping and negating, the contrapositive is
Umbrella. Flipping and negating, the contrapositive is ![]() Umbrella
Umbrella ![]()
![]() Raining. If I don’t have my umbrella, what can we conclude? Well, certainly it must not be raining.
Raining. If I don’t have my umbrella, what can we conclude? Well, certainly it must not be raining.
One final note before moving on from contrapositives from the time being: The contrapositive of the contrapositive is the original statement (![]()
![]()
![]()
![]()
![]()
![]()
![]() ). Once again we’re left with a light switch to flip back and forth but no real ability to move further through an argument. One more tool is required.
). Once again we’re left with a light switch to flip back and forth but no real ability to move further through an argument. One more tool is required.
The ![]() Transitive
Transitive ![]() Property
Property
Compared to the contrapositive, the transitive property of arrow diagrams is wildly intuitive to most students. Almost everyone will correctly deduce the property given the conditions in which it applies. However, application of the transitive property is not without its perils, and caution and developed understanding are required.
The transitive property states that:
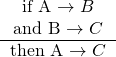
Two arrow diagrams can be linked together into longer chains if the end of one arrow diagram exactly matches the start of the other.
The order of the diagrams isn’t important:
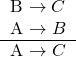
…is every bit as valid.
However, the direction of the arrows is critical:
![]()
…gives you nothing.
Furthermore, the requirement of an exact match between the end of one diagram and the start of another isn’t at all flexible.
The LSAT can make subtle switches from “special needs” to “disabled” or “acceptable” to “accurate,” and they’re easy to overlook because of the way our minds work. We’ve all been trained that it’s important in writing and speaking to vary our terms. Good communicators use synonyms to avoid saying the same things in the same ways over and over and boring their readers and/or listeners to tears. Consequently, we have been trained as readers and as listeners to assume that any minor variation of terms is nothing more than the expected use of synonyms.
On the LSAT, though, such a switch can hide the key to an entire question. It’s like having a plane ticket from Atlanta to Baltimore and a plane ticket from Boston to Chicago. Good luck getting from point A to point C if that’s all you’ve got.
Qualifiers like “some” can also screw up the transitive property connection. It is tempting to assume that if ![]() and
and ![]()
![]() then, surely, at least
then, surely, at least ![]()
![]() . However,
. However, ![]() and
and ![]()
![]() are not the same thing, and no conclusion is warranted here.
are not the same thing, and no conclusion is warranted here.
The following picture represents ![]() :
:
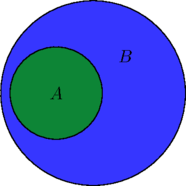
Let’s consider how the statement ![]()
![]() might be added to the picture.
might be added to the picture.
Maybe it looks like this:
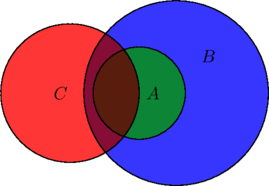
Here, indeed, some ![]() s are
s are ![]() s.
s.
But it could also look like this:
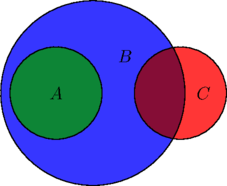
In this case, it seems that in fact NO ![]() s are
s are ![]() s.
s.
The picture could even look like this:
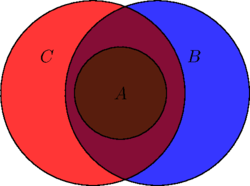
In this final case, ALL ![]() s are
s are ![]() s.
s.
Clearly, no conclusion was warranted by combining the statements ![]() and
and ![]()
![]() .
.
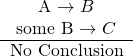
Although pictures helped to test the arrow diagrams against our intuitions in this case, it is not generally recommended to resort to picture-drawing. The pictures here confirmed that the transitive property, applied correctly, gave the right result. And indeed it always will. If the arrow diagrams don’t connect, if the link between the end of one diagram and the start of the next is not exact, then there is no conclusion — period. So it’s best to just use the arrow diagrams and skip the rest.
As we wrap up the issue of qualifiers and the transitive property, note that the inclusion of a word like “some” doesn’t automatically kill a prospective conclusion. The propositions that connect the two diagrams have to be identical, but a qualifier that does not affect this connection causes no problems for the transitive property. The following structure, for instance, is entirely valid:
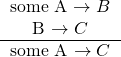
Translating to Formal Logic
In order to put these wonderful tools to use, it’s necessary to first translate statements from plain English into formal logic. The only problem is that English is a messy, confusing language that doesn’t always express ideas either consistently or in order. Students who attempt to translate statements by reading from left to right will find themselves frequently disappointed.
Instead, the goal should be to think critically about what the wording in question means to say and attempt to paraphrase it into an if/then statement if possible. Recall that the statement “if ![]() , then
, then ![]() ” is wholly equivalent to the arrow diagram
” is wholly equivalent to the arrow diagram ![]() . Because if/then statements directly translate to arrow diagrams, they serve as useful bridges between English and formal logic.
. Because if/then statements directly translate to arrow diagrams, they serve as useful bridges between English and formal logic.
A straightforward example is the statement “all members of Pteropsida are tracheophytes,” which paraphrases as “if it’s a member of Pteropsida then it’s a tracheophyte” and therefore translates as ![]() .
.
Only slightly more complicated is “without meaningful emotional connections to others we feel isolated.” That proposition can be rephrased as “if not meaningful emotional connections, then feel isolated,” or ![]() .
.
However, other statements are much trickier.
Consider the statement “unless the polls are grossly inaccurate, Slater will win.” Basically, “if the polls are not not accurate, then Slater will win”: ![]()
![]()
![]() .
.
Worse still, try “no strictly physical theory can explain consciousness.” It may be tempting to translate from left to right as ![]() — but read that arrow diagram back in English; it says “if it’s not a physical theory, then it explains consciousness.” That’s certainly not what we meant. Instead, if we had translated to an if/then statement first, we might have realized that we meant something more along the lines of “if it is a physical theory, then it cannot explain consciousness”;
— but read that arrow diagram back in English; it says “if it’s not a physical theory, then it explains consciousness.” That’s certainly not what we meant. Instead, if we had translated to an if/then statement first, we might have realized that we meant something more along the lines of “if it is a physical theory, then it cannot explain consciousness”; ![]() is the correct translation.
is the correct translation.
Let’s do one more like these: “one cannot prepare a good meal from bad soil.” This statement again presents the temptation to blunder into ![]() (“not a good meal implies not good soil”), but it’s backwards. Instead, this statement means that “if good meal, then good soil” and the correct arrow diagram
(“not a good meal implies not good soil”), but it’s backwards. Instead, this statement means that “if good meal, then good soil” and the correct arrow diagram ![]() is exactly the reverse of (and certainly not equivalent to) the tempting mistake. Rest assured that a wrong answer featuring the incorrect reversed arrow diagram lurks in the answer choices awaiting students who are led astray in this manner.
is exactly the reverse of (and certainly not equivalent to) the tempting mistake. Rest assured that a wrong answer featuring the incorrect reversed arrow diagram lurks in the answer choices awaiting students who are led astray in this manner.
Finally, be aware that not all logical statements involve arrows. A statement like “used pop is on sale” should simply be expressed as ![]() . Similarly, “no students with learning disabilities have yet enrolled in the school” is probably best written
. Similarly, “no students with learning disabilities have yet enrolled in the school” is probably best written ![]() , depending on surrounding context.
, depending on surrounding context.
Example Time
Let’s try PrepTest 35, Section 1, Question 22 (Next 10 LSAT, page 226).
The first statement is the tricky one here, and the temptation is to diagram it from left to right as ![]() . However, this statement reads “if it’s not a chordate, then it’s a tracheophyte,” and that’s certainly not what the given statement says or means. Instead, try to paraphrase into an if/then statement. One statement that works is “if it’s a chordate, then it’s not a tracheophyte.” A correct arrow diagram for this statement is
. However, this statement reads “if it’s not a chordate, then it’s a tracheophyte,” and that’s certainly not what the given statement says or means. Instead, try to paraphrase into an if/then statement. One statement that works is “if it’s a chordate, then it’s not a tracheophyte.” A correct arrow diagram for this statement is ![]() .
.
The second premise is easily diagrammed as ![]() .
.
The third statement, the conclusion of the argument, is trickier again, but following the process used for the first statement we can paraphrase it as “if it’s in Pteropsida, then it’s not in Hominidae.” The resulting (and correct) diagram is ![]() .
.
To review, the given statements can be diagrammed as:
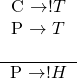
Although at first glance it may seem that the premises don’t connect at all, taking the contrapositive of statement 1 solves that problem nicely:
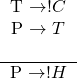
Now the transitive property connects from the end of statement 2 to the beginning of statement 1; the result is ![]() . However, we’re still a step away from our conclusion; we have to find a way to go from
. However, we’re still a step away from our conclusion; we have to find a way to go from ![]() to
to ![]() .
.
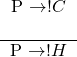
The missing link is ![]() :
:
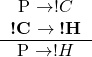
In other words, we need “if it’s not a chordate, then it’s not in Hominidae.” A quick scan of the answer choices reveals no such proposition. But remember, the contrapositive of the desired statement works just as well — and in fact we might have expected that the positive version would be more likely to show up in the answers. The contrapositive of ![]() is
is ![]() . In English, “if it’s in Hominidae, then it’s a chordate.” Happily, this proposition is present in the answer choices — it’s B, and answer B is correct.
. In English, “if it’s in Hominidae, then it’s a chordate.” Happily, this proposition is present in the answer choices — it’s B, and answer B is correct.
The Section Wherein Relevant LSAT Questions Are Listed
There’s no shortage of formal logic-based questions on the LSAT. Here’s a moderately thorough list from the two most recent books of LSAT PrepTests:
- PrepTest 30, Section 1, Questions 6-10 (Next 10 LSAT, page 51)
PrepTest 30, Section 2, Question 18 (Next 10 LSAT, page 59)
PrepTest 30, Section 4, Question 1 (Next 10 LSAT, page 70)
PrepTest 30, Section 4, Question 9 (Next 10 LSAT, page 72)
PrepTest 30, Section 4, Question 18 (Next 10 LSAT, page 75)
PrepTest 31, Section 2, Question 10 (Next 10 LSAT, page 91)
PrepTest 32, Section 1, Question 7 (Next 10 LSAT, page 120)
PrepTest 32, Section 4, Question 4 (Next 10 LSAT, page 139)
PrepTest 33, Section 1, Question 15 (Next 10 LSAT, page 156)
PrepTest 33, Section 1, Question 23 (Next 10 LSAT, page 158)
PrepTest 33, Section 4, Questions 6-12 (Next 10 LSAT, page 177)
PrepTest 34, Section 2, Question 10 (Next 10 LSAT, page 196)
PrepTest 34, Section 2, Question 23 (Next 10 LSAT, page 200)
PrepTest 34, Section 3, Question 10 (Next 10 LSAT, page 204)
PrepTest 34, Section 3, Question 23 (Next 10 LSAT, page 208)
PrepTest 34, Section 4, Questions 19-24 (Next 10 LSAT, page 213)
PrepTest 35, Section 1, Question 20 (Next 10 LSAT, page 225)
PrepTest 35, Section 4, Question 14 (Next 10 LSAT, page 244)
PrepTest 36, Section 1, Question 11 (Next 10 LSAT, page 257)
PrepTest 36, Section 1, Question 14 (Next 10 LSAT, page 258)
PrepTest 36, Section 1, Question 18 (Next 10 LSAT, page 259)
PrepTest 36, Section 1, Question 22 (Next 10 LSAT, page 260)
PrepTest 36, Section 3, Question 12 (Next 10 LSAT, page 273)
PrepTest 36, Section 3, Question 17 (Next 10 LSAT, page 275)
PrepTest 36, Section 3, Question 19 (Next 10 LSAT, page 275)
PrepTest 36, Section 4, Questions 1-6 (Next 10 LSAT, page 278)
PrepTest 37, Section 2, Question 3 (Next 10 LSAT, Page 296)
PrepTest 37, Section 2, Question 5 (Next 10 LSAT, page 297)
PrepTest 37, Section 2, Question 12 (Next 10 LSAT, page 299)
PrepTest 37, Section 3, Question 3 (Next 10 LSAT, page 304)
PrepTest 37, Section 4, Question 9 (Next 10 LSAT, page 310)
PrepTest 37, Section 4, Question 20 (Next 10 LSAT, page 313)
PrepTest 38, Section 1, Question 20 (Next 10 LSAT, page 327)
PrepTest 38, Section 4, Question 16 (Next 10 LSAT, page 346)
- PrepTest 52, Section 1, Question 3 (10 New LSAT, page 9)
PrepTest 52, Section 1, Question 17 (10 New LSAT, page 12)
PrepTest 52, Section 3, Question 15 (10 New LSAT, page 24)
PrepTest 52, Section 3, Question 24 (10 New LSAT, page 27)
PrepTest 53, Section 1, Question 21 (10 New LSAT, page 50)
PrepTest 53, Section 3, Question 12 (10 New LSAT, page 59)
PrepTest 53, Section 3, Question 19 (10 New LSAT, page 61)
PrepTest 54, Section 2, Question 13 (10 New LSAT, page 91)
PrepTest 54, Section 2, Question 23 (10 New LSAT, page 94)
PrepTest 54, Section 2, Question 26 (10 New LSAT, page 95)
PrepTest 54, Section 3, Questions 1-5 (10 New LSAT, page 96)
PrepTest 54, Section 4, Question 22 (10 New LSAT, page 106)
PrepTest 54, Section 4, Question 23 (10 New LSAT, page 106)
PrepTest 55, Section 1, Question 12 (10 New LSAT, page 119)
PrepTest 55, Section 1, Question 15 (10 New LSAT, page 120)
PrepTest 55, Section 1, Question 25 (10 New LSAT, page 123)
PrepTest 55, Section 3, Question 20 (10 New LSAT, page 138)
PrepTest 55, Section 3, Question 23 (10 New LSAT, page 139)
PrepTest 56, Section 2, Question 23 (10 New LSAT, page 162)
PrepTest 56, Section 3, Question 16 (10 New LSAT, page 168)
PrepTest 57, Section 2, Question 7 (10 New LSAT, page 194)
PrepTest 57, Section 2, Question 12 (10 New LSAT, page 195)
PrepTest 57, Section 2, Question 19 (10 New LSAT, page 197)
PrepTest 57, Section 3, Question 19 (10 New LSAT, page 205)
PrepTest 57, Section 3, Question 20 (10 New LSAT, page 206)
PrepTest 57, Section 3, Question 24 (10 New LSAT, page 207)
PrepTest 58, Section 1, Question 25 (10 New LSAT, page 231)
PrepTest 58, Section 3, Questions 7-12 (10 New LSAT, page 241)
PrepTest 58, Section 4, Question 19 (10 New LSAT, page 249)
PrepTest 58, Section 4, Question 24 (10 New LSAT, page 251)
PrepTest 59, Section 1, Questions 11-16 (10 New LSAT, page 262)
PrepTest 59, Section 2, Question 16 (10 New LSAT, page 268)
PrepTest 59, Section 2, Question 17 (10 New LSAT, page 268)
PrepTest 59, Section 2, Question 26 (10 New LSAT, page 271)
PrepTest 59, Section 3, Question 10 (10 New LSAT, page 275)
PrepTest 59, Section 3, Question 19 (10 New LSAT, page 277)
PrepTest 60, Section 1, Question 3 (10 New LSAT, page 296)
PrepTest 60, Section 1, Question 21 (10 New LSAT, page 302)
PrepTest 60, Section 3, Question 3 (10 New LSAT, page 309)
PrepTest 60, Section 3, Question 10 (10 New LSAT, page 310)
PrepTest 60, Section 3, Question 12 (10 New LSAT, page 311)
PrepTest 61, Section 2, Question 3 (10 New LSAT, page 341)
PrepTest 61, Section 2, Question 13 (10 New LSAT, page 343)
PrepTest 61, Section 2, Question 23 (10 New LSAT, page 346)
PrepTest 61, Section 2, Question 24 (10 New LSAT, page 347)
PrepTest 61, Section 4, Question 25 (10 New LSAT, page 359)
Tags: Analytical Reasoning, Formal Logic, Logical Reasoning, LSAT